APTITUDE | ARITHMATICAL | HEIGHTS AND DISTANCE | PROBLEMS BASED ON DISTANCES 1

DIRECTIONS : Problems based on distances.

1.	A ladder learning against a wall makes an angle of 60° with the ground. If the length of the ladder is 19 m, find the distance of the foot of the ladder from the wall.
	A.   9 m	B.   9.5 m
	C.  10.5 m	D.  12 m

Solution

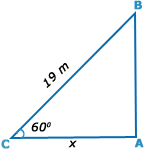Let AB be the wall and BC be the ladder. Then, < ABC = 60° and, BC = 19 m.; AC = x metres AC/BC = cos 60° = x / 19 =1 / 2 x= 19/2 = 9.5 m.

2.	The angle of elevation of a ladder leaning against a wall is 60° and the foot of the ladder is 4.6 m away from the wall. The length of the ladder is
	A.  2.3 m	B.  4.6 m
	C.  7.8 m	D.  9.2 m

Solution

Let AB be the wall and BC be the ladder. 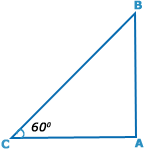Then, < ABC = 60° AC = 4.6 m.; AC/BC = cos 60° = 1 /2 ‹=›BC=2×AC =(2× 4.6) m =9.2 m

3.	The angle of elevation of the sun, when the length of the shadow of a tree is √3 times the height of the tree is
	A.   30°	B.   45°
	C.  60°	D.  90°

Solution

Let AB be the tree and AC be its shadow. 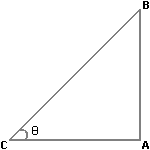Then, < ABC = θ. Then, AC/AB = √3 cotθ= √3 θ=30°

4.	If the height of a pole is 2√3 metres and the length of its shadow is 2 metres, find the angle of elevation of the sun.
	A.  30°	B.  45°
	C.  60°	D.  90°

Solution

Let AB be the pole and AC be its shadow. 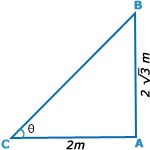Then, < ACB = θ. Then, AB= 2 √3 m, AC = 2m, tanθ= AB/AC=2√3/2 = √3 θ=60°

5.	From a point P on a level ground, the angle of elevation of the top tower is 30°. If the tower is 100 m high, the distance of point P from the foot of the tower is:
	A.  149 m	B.  156 m
	C.  173 m	D.  200 m

Solution

Let AB be the tower. 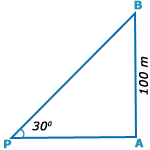Then, <APB =30° and AB= 100 m AB/AP= tan30° = 1 / √3 AB = (AB x √3)= 100√3 m. = (100 x 1.73) m = 173 m.